Deep Learning学习笔记整理(六)

　　Artificial Intelligence，也就是人工智能，就像长生不老和星际漫游一样，是人类最美好的梦想之一。

声明：

该Deep Learning的学习系列是整理自网上很大牛和机器学习专家所无私奉献的资料的。具体引用的资料请看参考文献。具体的版本声明也参考原文献。
本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益，还望海涵，并联系博主删除。
本人才疏学浅，整理总结的时候难免出错，还望各位前辈不吝指正，谢谢。
阅读本文需要机器学习、计算机视觉、神经网络等等基础（如果没有也没关系了，没有就看看，能不能看懂，呵呵）。
此属于第一版本，若有错误，还需继续修正与增删。还望大家多多指点。大家都共享一点点，一起为祖国科研的推进添砖加瓦（呵呵，好高尚的目标啊）。请联系：zouxy09@qq.com
转自网络^【1】

　　假设有一个二部图，每一层的节点之间没有链接，一层是可视层，即输入数据层（v)，一层是隐藏层(h)，如果假设所有的节点都是随机二值变量节点（只能取0或者1值），同时假设全概率分布p(v,h)满足Boltzmann 分布，我们称这个模型是Restricted BoltzmannMachine (RBM)。

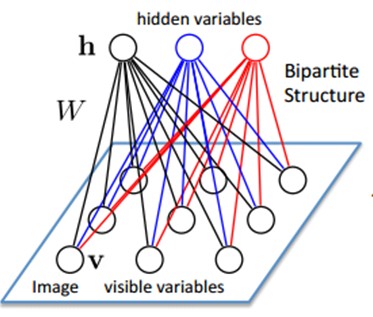
　　下面我们来看看为什么它是Deep Learning方法。首先，这个模型因为是二部图，所以在已知v的情况下，所有的隐藏节点之间是条件独立的（因为节点之间不存在连接），即p(h丨v)=p(h1丨v)…p(hn丨v)。同理，在已知隐藏层h的情况下，所有的可视节点都是条件独立的。同时又由于所有的v和h满足Boltzmann 分布，因此，当输入v的时候，通过p(h丨v) 可以得到隐藏层h，而得到隐藏层h之后，通过p(v丨h)又能得到可视层，通过调整参数，我们就是要使得从隐藏层得到的可视层v1与原来的可视层v如果一样，那么得到的隐藏层就是可视层另外一种表达，因此隐藏层可以作为可视层输入数据的特征，所以它就是一种Deep Learning方法。

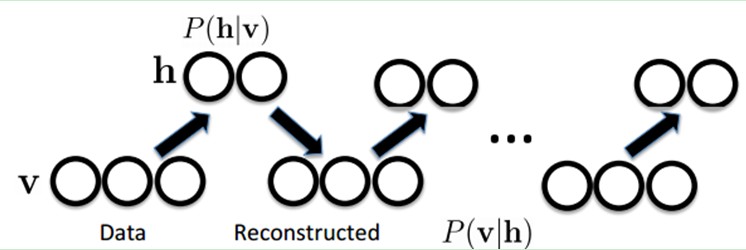
　　如何训练呢？也就是可视层节点和隐节点间的权值怎么确定呢？我们需要做一些数学分析。也就是模型了。

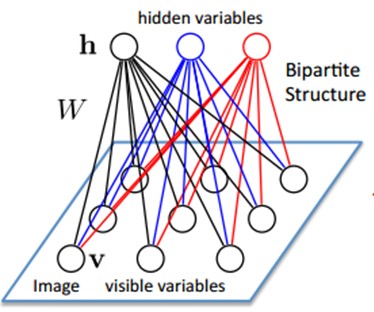
　　联合组态（jointconfiguration）的能量可以表示为：

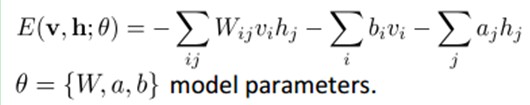
　　而某个组态的联合概率分布可以通过Boltzmann 分布（和这个组态的能量）来确定：

　　因为隐藏节点之间是条件独立的（因为节点之间不存在连接），即：

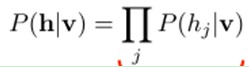
　　然后我们可以比较容易（对上式进行因子分解Factorizes）得到在给定可视层v的基础上，隐层第j个节点为1或者为0的概率：

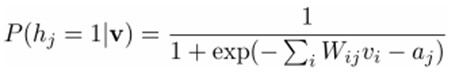
　　同理，在给定隐层h的基础上，可视层第i个节点为1或者为0的概率也可以容易得到：

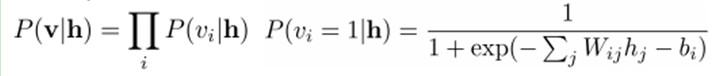
　　给定一个满足独立同分布的样本集：D={v⁽¹⁾, v⁽²⁾,…, v^(N)}，我们需要学习参数θ={W,a,b}。

　　我们最大化以下对数似然函数（最大似然估计：对于某个概率模型，我们需要选择一个参数，让我们当前的观测样本的概率最大）：

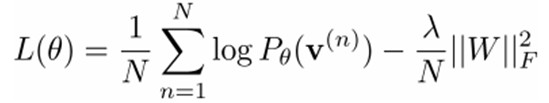
　　也就是对最大对数似然函数求导，就可以得到L最大时对应的参数W了。

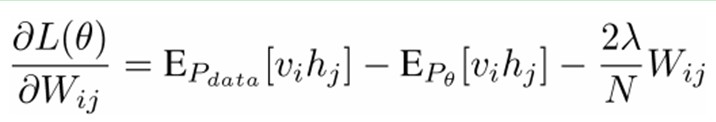
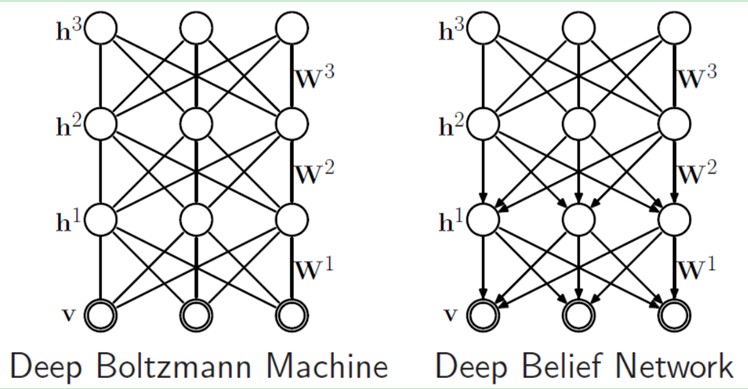
　　如果，我们把隐藏层的层数增加，我们可以得到Deep Boltzmann Machine(DBM)；如果我们在靠近可视层的部分使用贝叶斯信念网络（即有向图模型，当然这里依然限制层中节点之间没有链接），而在最远离可视层的部分使用Restricted Boltzmann Machine，我们可以得到DeepBelief Net（DBN）。

9.4、Deep Belief Networks深信度网络

　　DBNs是一个概率生成模型，与传统的判别模型的神经网络相对，生成模型是建立一个观察数据和标签之间的联合分布，对P(Observation

Label)和 P(Label

Observation)都做了评估，而判别模型仅仅而已评估了后者，也就是P(Label

Observation)。对于在深度神经网络应用传统的BP算法的时候，DBNs遇到了以下问题：

　　（1）需要为训练提供一个有标签的样本集；

　　（2）学习过程较慢；

　　（3）不适当的参数选择会导致学习收敛于局部最优解。

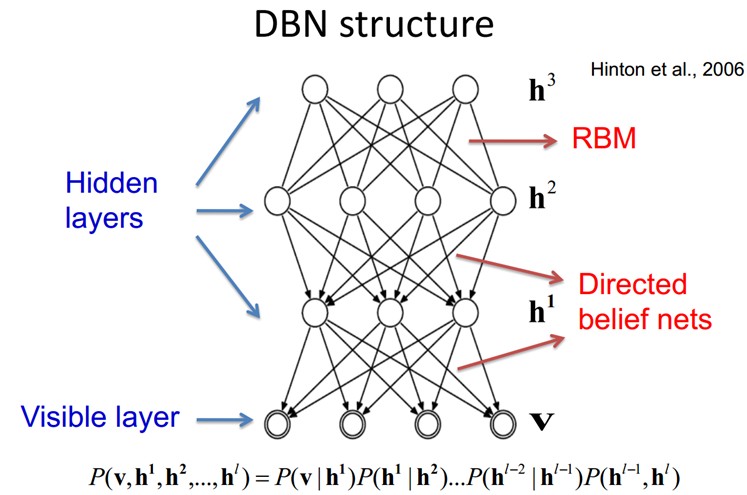
　　DBNs由多个限制玻尔兹曼机（Restricted Boltzmann Machines）层组成，一个典型的神经网络类型如图三所示。这些网络被“限制”为一个可视层和一个隐层，层间存在连接，但层内的单元间不存在连接。隐层单元被训练去捕捉在可视层表现出来的高阶数据的相关性。

　　首先，先不考虑最顶构成一个联想记忆（associative memory）的两层，一个DBN的连接是通过自顶向下的生成权值来指导确定的，RBMs就像一个建筑块一样，相比传统和深度分层的sigmoid信念网络，它能易于连接权值的学习。

　　最开始的时候，通过一个非监督贪婪逐层方法去预训练获得生成模型的权值，非监督贪婪逐层方法被Hinton证明是有效的，并被其称为对比分歧（contrastive divergence）。

　　在这个训练阶段，在可视层会产生一个向量v，通过它将值传递到隐层。反过来，可视层的输入会被随机的选择，以尝试去重构原始的输入信号。最后，这些新的可视的神经元激活单元将前向传递重构隐层激活单元，获得h（在训练过程中，首先将可视向量值映射给隐单元；然后可视单元由隐层单元重建；这些新可视单元再次映射给隐单元，这样就获取新的隐单元。执行这种反复步骤叫做吉布斯采样）。这些后退和前进的步骤就是我们熟悉的Gibbs采样，而隐层激活单元和可视层输入之间的相关性差别就作为权值更新的主要依据。

　　训练时间会显著的减少，因为只需要单个步骤就可以接近最大似然学习。增加进网络的每一层都会改进训练数据的对数概率，我们可以理解为越来越接近能量的真实表达。这个有意义的拓展，和无标签数据的使用，是任何一个深度学习应用的决定性的因素。

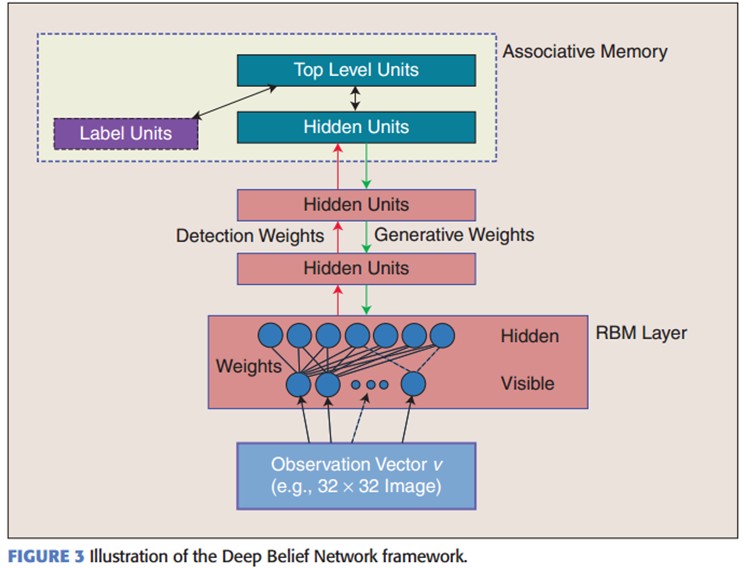
　　在最高两层，权值被连接到一起，这样更低层的输出将会提供一个参考的线索或者关联给顶层，这样顶层就会将其联系到它的记忆内容。而我们最关心的，最后想得到的就是判别性能，例如分类任务里面。

　　在预训练后，DBN可以通过利用带标签数据用BP算法去对判别性能做调整。在这里，一个标签集将被附加到顶层（推广联想记忆），通过一个自下向上的，学习到的识别权值获得一个网络的分类面。这个性能会比单纯的BP算法训练的网络好。这可以很直观的解释，DBNs的BP算法只需要对权值参数空间进行一个局部的搜索，这相比前向神经网络来说，训练是要快的，而且收敛的时间也少。

　　DBNs的灵活性使得它的拓展比较容易。一个拓展就是卷积DBNs（Convolutional Deep Belief Networks(CDBNs)）。DBNs并没有考虑到图像的2维结构信息，因为输入是简单的从一个图像矩阵一维向量化的。而CDBNs就是考虑到了这个问题，它利用邻域像素的空域关系，通过一个称为卷积RBMs的模型区达到生成模型的变换不变性，而且可以容易得变换到高维图像。DBNs并没有明确地处理对观察变量的时间联系的学习上，虽然目前已经有这方面的研究，例如堆叠时间RBMs，以此为推广，有序列学习的dubbed temporal convolutionmachines，这种序列学习的应用，给语音信号处理问题带来了一个让人激动的未来研究方向。

　　目前，和DBNs有关的研究包括堆叠自动编码器，它是通过用堆叠自动编码器来替换传统DBNs里面的RBMs。这就使得可以通过同样的规则来训练产生深度多层神经网络架构，但它缺少层的参数化的严格要求。与DBNs不同，自动编码器使用判别模型，这样这个结构就很难采样输入采样空间，这就使得网络更难捕捉它的内部表达。但是，降噪自动编码器却能很好的避免这个问题，并且比传统的DBNs更优。它通过在训练过程添加随机的污染并堆叠产生场泛化性能。训练单一的降噪自动编码器的过程和RBMs训练生成模型的过程一样。

　　未完待续

参考

【1】 http://blog.csdn.net/zouxy09/article/details/8775360

Deep Learning学习笔记整理(六)

声明：

目录：

9.3、Restricted Boltzmann Machine (RBM)限制波尔兹曼机

9.4、Deep Belief Networks深信度网络

参考