超级电容设计

超级电容模块作为电源到底盘电机中间的功率控制模块，要求完成以下任务：限制电源的输出功率，做到功率实时监控和动态调整；利用电机组功率消耗的谷值时间给超级电容组充电，以达到能量合理分配和利用的目的；实时汇报给操作手超级电容当前电量，方便操作手进行调整。

一、需求确定

1.1、总体需求

　超级电容模块作为电源到底盘电机中间的功率控制模块，要求完成以下任务：
1、限制电源的输出功率，做到功率实时监控和动态调整。
2、利用电机组功率消耗的谷值时间给超级电容组充电，以达到能量合理分配和利用的目的。
3、实时汇报给操作手超级电容当前电量，方便操作手进行调整。

1.2、具体需求

　电路主要分为三个大类：1、电源线路 2、检测线路 3、控制电路。
1、电源线路
Ⅰ.BUCK降压转换器：通过控制转换器输出电压来限制输出功率，达到控制输入功率目的（必需）
Ⅱ.BOOST升压转换器：将电源升压给超级电容充电（必需）
Ⅲ.各个芯片的供电电源模块（必需）
2、检测线路
Ⅰ.电流检测模块：总的输入和输出电流（必需）
Ⅱ.电压检测模块：输入电压，输出电压和超级电容电压（必需）
3、控制电路
把检测电路得到的数据输入给STM32芯片，通过运算输出控制量
Ⅰ.计算输入和输出功率（必需）
Ⅱ.使用输入功率与当前等级的限制功率比较，计算BUCK转换器的PWM的占空比（必需）
Ⅲ.使用电容电压计算其剩余电量，发送给操作手，由他控制超级电容放电（必需）
Ⅳ.使用输出功率与一定值作比较，和电容电压共同控制超级电容的充电（必需）

图1 电路框图

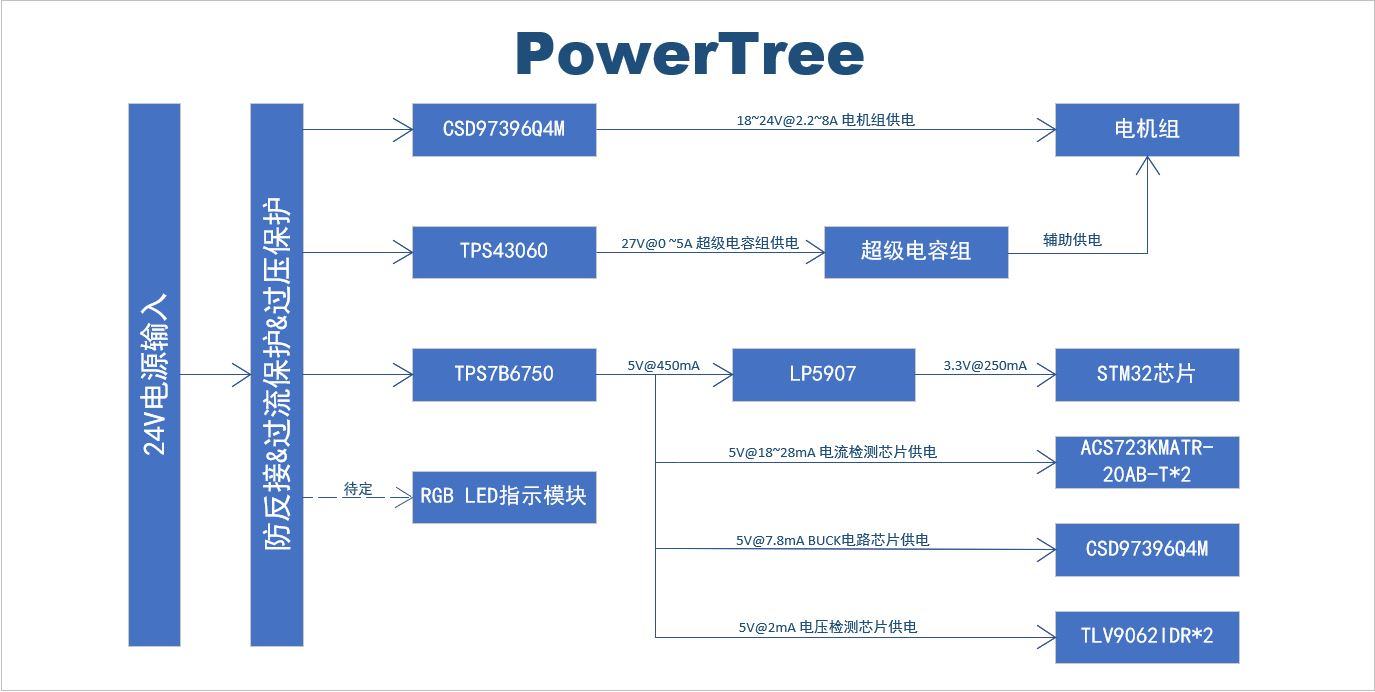
二、电路参数实际计算

2.1、效率分析

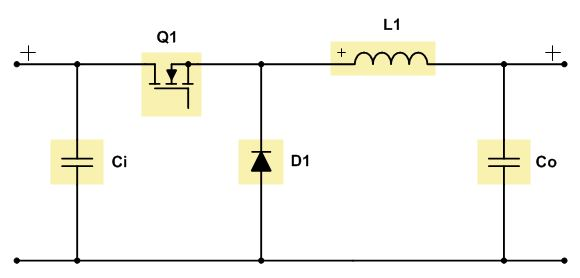
图1 非同步BUCK电路

　测试电路采用非同步BUCK电路，输出电压值18~24V，测试频率1kHz，负载连接一个无刷直流电机，预计转换效率在95%左右(仿真结果)。实际转换效率75%左右，同时电压有明显波动，但对电机的运动未造成巨大影响（也可能受实验参数限制，未观察出影响）。
　分析：由于测试所使用电路相当简单，不存在电路本身结构造成功率损失的问题。于是将问题矛头指向MOS管，二极管和电感这三个元件造成的损耗。测得MOS管IRFP250N的 $R_{DS(ON)}$ 在75mΩ左右，二极管10A10的 $V_F$ 最大为1V，铁氧体芯电感(双1.2线，10mH)的DCR在110mΩ左右。
计算MOS管的损耗：
MOS管在1KHz频率下的主要损耗为：

$P_D = P_{CON} + P_{SW\_OPEN} + P_{SW\_CLOSE} (2-1-1)$

其中 $P_{CON}$ 为导通损耗， $P_{SW\_OPEN}$ 为开通损耗， $P_{SW\_CLOSE}$ 为关断损耗。
$P_{CON}$ 的计算通式为（取占空比的中间值的导通损耗为准）：

$P_{CON} = I_{DS}^2 \ast R_{DS(ON)} \ast D = 1.75^2 \times 0.075 \times 0.875 \approx 0.1148W (2-1-2)$

$P_{SW\_OPEN}$

和 $P_{SW\_CLOSE}$ 的计算过程若是较真起来会相当复杂，这里先采用近似最坏假设计算：

$\begin{equation}\begin{split} P_{SW\_OPEN}&= \frac 12 \ast V_{DS} \ast I_{DS} \ast (T_r + T_{d(ON)})\\ &\frac 12 \times 0.075 \times 1000 \times (14 + 43) \times 10^{-9} = 0.0065mW\\ \end{split}\end{equation} (2-1-3)$

$\begin{equation}\begin{split} P_{SW\_CLOSE}&= \frac 12 \ast V_{DS} \ast I_{DS} \ast (T_f + T_{d(OFF)})\\ &\frac 12 \times 0.075 \times 1000 \times (14 + 33) \times 10^{-9} = 0.0085mW\\ \end{split}\end{equation} (2-1-4)$

其中 $V_{DS}$ 为导通压降， $I_{DS}$ 为平均电流， $T_r$ ， $T_{d(ON)}$ ， $T_f$ 和 $T_{d(OFF)}$ 分别为上升时间，开通延迟时间，下降时间和关断延迟时间。
总损耗：

$P_D = P_{CON} + P_{SW\_OPEN} + P_{SW\_CLOSE} = 0.1148 + (0.0065 + 0.0085) \times 10^(-3) \approx 0.1148W (2-1-5)$

计算二极管的损耗,这里以二极管的最大损耗为准：

$P_D = V_F \ast I_F \ast (1 - D) = 1 \times 1.75 \times (1 - 0.75) = 0.4375W (2-1-6)$

其中 $V_F$ 为导通压降， $I_F$ 为导通电流，D为占空比
计算电感的损耗：
电感的铜损：

$P_{Cu} = I_F^2 \ast DCR = 1.752 \times 0.11 \approx 0.3369W (2-1-7)$

其中 $I_F$ 为导通电流，DCR为电感直流电阻
电感的铁损：
注意：这里的公式是大量简化后得到的,同时忽略了涡流损耗，原因是电感体积较小，具体分析根据文献[1]。实际计算公式是基于 Steinmetz方程修正得到的，但该修正方程的参数难以获得，故使用简化方程。假设电路工作在CCM（电流连续）模式下，仍然以占空比中间值计算，则:

$励磁B_{PP}^{+} = \frac {(U_i - U_o) \ast D \ast T}{N \ast A_e} = \frac {(24 - 21) \times 0.875 X 1 \times 10^{-3}}{28 \times (31 - 19) \times 13 \times 10^{-4}} \approx 6.0096 \times 10^{-3}Wb (2-1-8)$

$退磁B_{PP}^{-} = \frac {U_o \ast (1 - D) \ast T}{N \ast A_e} = \frac {21 X 0.125 \times 1 \times 10^{-3}}{28 \times (31 - 19) \times 13 \times 10^{-4}} \approx 6.0096 \times 10^{-3}Wb (2-1-9)$

$P_{Fe} = B_{PP}^{2} \ast f = (6.0096 \times 10^{-3})^2 \times 1000 \approx 0.0361W (2-1-10)$

$B_{PP}$ 为磁通变化量，D为占空比，T为周期，N为匝数， $A_e$ 为磁芯横截面积， $U_i$ ， $U_o$ 分别为输入电压和输出电压，f为频率

$P_D = P_{Cu} + P_{Fe} = 0.3369 + 0.0361 = 0.3730W (2-1-11)$

综上，可知二极管的损耗是最大的，是由其不可忽略的导通压降带来的。但，这不意味着其它两个元件的损耗也是可以忽略的，我必须认识到，这里的频率只有1kHz，属于低频。根据MOS管计算损耗的公式可知，其损耗会随着开关频率的升高而升高，具体体现在开通损耗 $P_{SW\_OPEN}$ 和关断损耗 $P_{SW\_CLOSE}$ ，虽然现在这两个值可以忽略不计，但我要往高频化方向发展时，这两个量会变得相当可观。根据电感计算损耗的公式，同样可知，其损耗也会随频率的升高而升高。庆幸的是，根据文献[1]，铁损在占空比D大于0.5的情况下损耗低于小于0.5的情况。

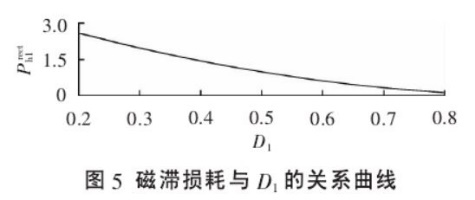
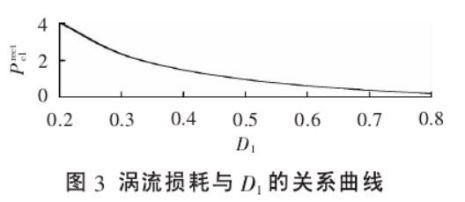
要说明的一点，电感的损耗计算可能误差会较大，市面上的电感本身标称误差就在±20%，且电磁场也是让分析变得难上加难。不过无妨，分析的过程本身是绝对正确的，可以一定程度反应实际情况，方便指导今后工作。而且，我在下面会介绍更好的器件损耗计算方法。最后，不通过计算，还有一种方法可以大致得知哪个元件损耗最大，即连通电源和负载后，放在桌面上半个小时，用手摸哪个发烫严重便可判断。

2.2、主要参数计算

查询过多方资料，得知这种非同步BUCK转换器的转换效率普遍不高，做得好的一般在80%以上。最后，在TI公司的资料里了解到同步BUCK转换器，通过替换二极管为MOS管大幅度减低导通压降。改进方案：
1、将电路替换为同步BUCK电路。控制难度会有所提升，但采用TI公司的一些器件可以达到稳定控制。（值得注意的是，同步电路并非完美，它在轻负载的情况下造成了不良的电路反应，即在高侧MOS管关断时，电感电流可能会倒流，但使用二极管不存在该问题，因此我选用的芯片有二极管仿真模式，价格也相对合理。）
2、提高开关频率，可以减小电感体积，提高能量密度，改善动态响应。（换用外径20mm的电感，原来的为31mm。）
3、采用软开关技术，减小由提高频率带来的开关损耗增加的问题。（尚未考虑周全，且计划先提升至10kHz，不算高频。）

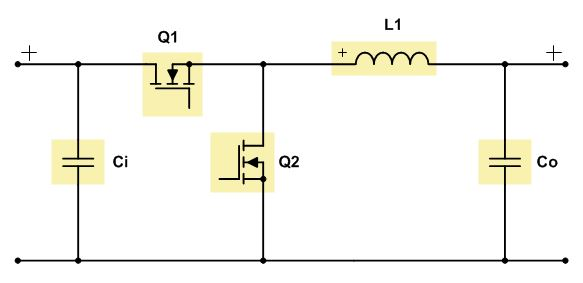
图4 同步BUCK电路

DC-DC转换电路外围电感选型需要考虑以下几个参数：
电感量L：L越大，储能能力越强，纹波越小，所需的滤波电容也就小。但是L越大，通常要求电感尺寸也会变大，DCR增加，导致DC-DC效率降低，相应的电感成本也会增加；
自谐频率 $f_0$ ：由于电感中存在寄生电容，使得电感存在一个自谐振频率。超过此f0是，电感表现为电容效应，低于此 $f_0$ ，电感才表现为电感效应（阻抗随频率增大而增加）；
直流电阻DCR：指产品电极之间所用漆包线的总的直流电阻，根据 $W=I^2R$ ，DCR可造成能量损耗，降低DC-DC效率，也是导致电感发热的主要原因；
交流电阻RAC：指电感量在指定频率下的电阻值，主要由电感线圈的直流电阻（交流下的集肤效应）、磁芯损耗以及介电损耗等组成，RAC越大，Q值越小；
饱和电流 $I_{sat}$ ：通常指电感量下降30%时对应的DC电流值；
温升电流 $I_{rms}$ ：通常指是电感表面温度上升40℃时的等效电流值；
这里我主要考虑L，DCR， $I_{sat}$ 和 $I_{rms}$ ，优先选择L，后三个主要和所用线的线径有关。

电感

电感值选用规则和计算公式：
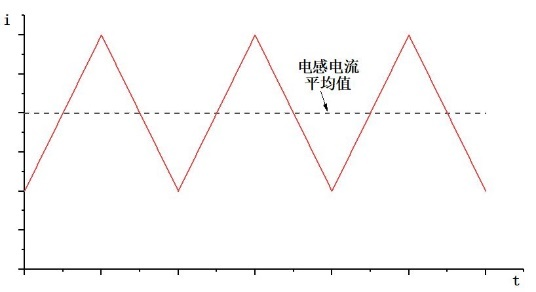
当MOS管打开时，电感电流线性上升，当MOS管关断时，电感电流线性下降，电感电流最大和最小值之差为电感纹波电流，该值也可以用输出负载电流乘以一个电流纹波系数r表示，即：

$∆I_L = \frac {(U_i - U_o) \ast D}{L_{临界} \ast f} = I_{out} \ast r (2-2-1)$

r一般在 0.3~0.5 之间。这里，我引入了一个重要的参数电流纹波系数r。为什么在算电感量之前要引入该参数？因为我要明确告诉后来人，这个参数远比电感值本身重要。
电流纹波系数r（参考文献[3]）定义：

$r = \frac {∆I}{I_L} \equiv 2 \times \frac {I_{AC}}{I_{DC}} (2-2-2)$

式（2-2-2）表示了电感电流的交流分量与直流分量的几何比例。其中 $∆I = 2 \ast I_{AC}$ ，一旦r确定，其他的所有参数几乎都能确定，因此，r值一定要清晰理解，仔细选择。电流纹波率r只适用于连续导通模式，有效值范围为0~2。显然，r=0时，电感无穷大，电流无波动，r=2时，转换器处于临界导通模式。我们当然希望输出的电流和电压都能平稳，所以，r值的取值便更偏向于取小（r并非越小越好）。在功率变换的计算中，我们通常用伏秒积表示电感在开关管开通关断过程中能量守恒。将式（2-2-3）代入式（2-2-2），得式（2-2-4）（2-2-5）：

$u = L \ast \frac {d_i}{d_t} (2-2-3)$

$r = \frac {∆I}{I_L} = \frac {E \ast t}{L \ast I_L } \equiv \frac {V_{ON} \ast D}{L \ast I_L \ast f} \equiv \frac {V_{OFF} \ast (1-D)}{L \ast I_L \ast f} (2-2-4)$

$L = \frac {V_{ON} \ast D}{r \ast I_L \ast f} 或 L \ast I_L = \frac {E \ast t}{r} (2-2-5)$

其中 $I_L$ 为电感电流， $V_{ON}$ 为开关管开通时的电感电压， $V_{OFF}$ 为关断时电感电压
最后，说明为何这个系数如此重要——因为它是基础量。实际情况中，L的取值由工况，开关频率，甚至是拓扑本身决定的。因此无法直接计算L。但是存在r值的一般设计经验，并已被广泛应用。任何情况下，r值都在0.3~0.5之间，其通常最优值为0.4，但不绝对，我就选了0.2。原因：电感尺寸没办法继续缩小了，纹波率太大反而增大滤波电容体积。（注：内容繁多，这只是相当简单的介绍，攫取了其中能快速解决问题的知识。）
按照式（2-2-5）选择电感值，这里 $D_{max} = \frac {U_o}{U_{i\_MIN}}$ 为最大占空比计算值，对于BUCK电路，存在固有的最大占空比 $D_{max}$ ，实际计算时选择两者中的较小值。

$L_{min} = \frac {U_{i\_{MAX}} - U_o \ast D_{max}}{I_L \ast r \ast f} = \frac {(25-18) \times 18}{2.2 \times 0.3 X 23.5 \times 10 \times 10^3} \approx 1.219mH (2-2-6)$

$I_{Lpeak} = I_L \ast (1 + \frac r2) = 7 \times (1 + \frac {0.2}{2}) = 7.7A (2-2-7)$

以上电感值是计算值最小值，随之得到的饱和电流 $I_{Lrms}$ 和峰值电流 $I_{Lpeak}$ 是最小值。按照工程上的要求，考虑到市面上的电感的标称值的误差通常在±20%，还考虑到当电感电流达到饱和电流时，电感值会下降25%，即：

$L_{chosen} = \frac {L_{min}}{0.8 \times 0.75} = \frac {1.219}{0.8 X 0.75} \approx 2.032mH (2-2-8)$

因此，我们只要选用比 $L_{chosen}$ 大的，满足峰值电流 $I_{Lpeak}$ 条件的电感。最后我决定选用2mH 1.2线的功率电感（DCR=11.55mΩ）。

电感损耗计算：

$P_{Cu} = I_Z^2 \ast DCR = 5^2 \times 11.55 = 288.75mW (2-2-9)$

$P_{Fe} = B_{PP}^2 \ast f = (14.9148 \times 10^{-3})^2 \times 10 ^4 \approx 2.2245W (2-2-10)$

$P_D = P_{Cu} + P_{Fe} = 0.28875 + 2.2245 =2.5133W (2-2-11)$

此外，我还推荐TI公司的一款软件Power Stage Designer Tool 4.0，该软件提供了相当全面的电路图。TI毕竟是业界的龙头，开关电源做得很好，很多资料都可以参考他们的。

电容

输入、输出滤波电容选用规则和计算公式（参考文献[2]），输出电容参数分析：
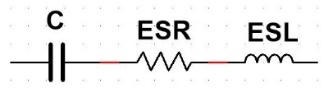
$C_o$ 很大的话，可以保证输出电压近似恒定，但是$C_o$很大会导致体积和成本更大。因此实际中根据容许的输出电压纹波来选择 $C_o$ 的值。设计时总是按照电感电流谐波全部进入 $C_o$ ，恒定分量进入负载（如果带阻性负载，在闭环电路的控制下，输出电压恒定，确实是这样的）。电感电流i的谐波进入电容，由电容的寄生电阻ESR、寄生电感ESL，和$C_o$值决定电压纹波的。对于低于500kHz的谐波，ESL产生的电压纹波可以忽略。因此，输出电容中由ESR和 $C_o$ 决定纹波电压分量。由ESR产生的纹波分量正比于电感电流纹波分量，由 $C_o$ 决定的纹波分量与流过电容的电流积分成正比。这两个分量相位是不同的。

对于BUCK，BOOST和BUCK-BOOST，其输出电容的最大有效值电流恰好都对应同一电压，而且该电压就是一般电感设计步骤中采用的电压值。即，对应BUCK的 $U_{i\_MAX}$ ，BOOST和BUCK-BOOST的 $U_{i\_MIN}$ 。因此，可直接使用由一般电感设计步骤的计算值。
另外，由于电容的ESR值对开关电源来说是一个很重要的值，过大会造成严重的电压尖峰，电容发热，电容失效等问题。通常，普通铝电解电容的ESR会达到欧姆级别。这里，我均选用贴片固态铝电解电容的ESR值（50mΩ：大致包括导线）计算。
输出电容参数计算：
此处设置的任务是同时满足下述三个约束条件（可自行调节）。
（1）最大输出纹波峰峰值小于输出电压的1%，即

$V_{o\_RIPPLE\_MAX} = 1% \ast U_{o\_{MAX}} = 1% \times 23.5 = 0.235V$

（2）负载突增时，可接受的最大电压下垂量为： $∆V_{DROP} = 1.175V$ ;
（3）负载突增时，可接受的最大超调量为： $V_{OVERSHOOT} = 1.175V$ ;
先计算选用的电感后的电流纹波率（式（2-2-12））和输出电流纹波峰峰值（式（2-2-13））：

$r_{Ui\_{MAX}} = \frac {U_{i\_{MAX}} - U_o \ast D_{max}} {I_o \ast L_{chosen} \ast f} = \frac {(25 - 18) \times 18}{2.2 \times 2 \times 10^{-3} \times 23.5 \times 10 X 10^3} \approx 0.12 （2-2-12）$

$I_{o\_RIPPLE\_MAX} = I_o \ast r_{Ui\_MAX} = 2.2 \times 0.12 = 0.2640A （2-2-13）$

得出电容寄生电阻ESR最大值，基于最大输出纹波：

$ESR \le \frac {V_{o\_RIPPLE\_MAX}}{I_o \ast r_{Ui \_ MAX}} = \frac {0.235}{2.2 \times 0.12} = 0.8902Ω （2-2-14）$

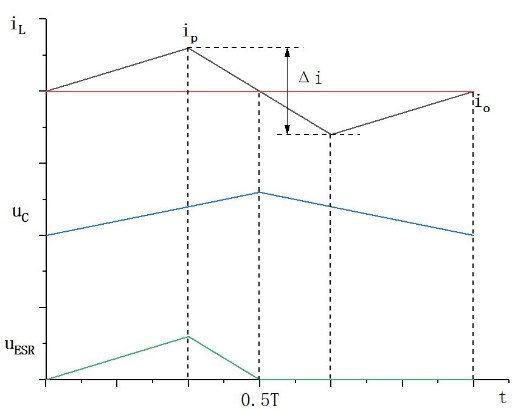
根据图2，电感电流在平均值以上的部分为滤波电容充电，其面积为 $∆S$ ，输出电容充电量 $∆Q$ ，根据能量守恒， $∆S= ∆Q$ ，通过式（2-2-15），（2-2-16），得到式（2-2-17）：

$∆S = \frac {1}{8f} \ast I_{o \_ RIPPLE \_ MAX} （2-2-15）$

$∆Q = C_o \ast V_{o \_ RIPPLE \_ MAX} （2-2-16）$

$C_{o\_1} \ge \frac {1}{8f} \ast \frac {I_{o\_RIPPLE\_MAX}}{V_{o\_RIPPLE\_MAX}} = \frac {1}{8 \times 10^4} \times \frac {2.2×0.12}{0.235} = 14.0425μF （2-2-17）$

同时，当负载发生变化时，假定输出电压需要2到3个开关周期返回到正常输出值，这段时间内不希望电压跌落至某一值。由 $I = C \frac {di}{dt}$ ，基于最大电压下垂量，可得式（2-2-18）：

$C \ge \frac {I_o \ast ∆t}{ V_{o\_RIPPLE\_MAX}} = \frac {2 \ast T \ast I_o}{∆V_{DROP}} = \frac {2 I_o}{∆V_{DROP} \ast f} （2-2-18）$

此处的下垂量与额外负载需求相关，因为正常负载需求在每个周期里都会被满足，电压不会下降。所以，此处的电流实际上对应增加的负载。

$C_{o\_2} \ge \frac {2 \ast ∆I_o}{∆V_{DROP} \ast f} = \frac {2 \times \frac 52}{1.175 \times 10^4} = 425.5319uF （2-2-19）$

最后，基于最大超调量，采用另一个标准：负载从最大负载$I_o$突变至0，所有的电感能量倾泻到输出电容中，升压到 $V_X$ ，同样，根据能量守恒，由式（2-2-20）推导出式（2-2-21）。

$\frac 12 \ast C \ast (V_x^2 - V_o^2) = \frac 12 \ast L \ast I_o^2 （2-2-20）$

$C\ge \frac {L \ast I_o^2}{(V_x + V_o ) \ast (V_x - V_o )} \approx \frac {L \ast I_o^2}{2 \ast V_o \ast ∆V_{OVERSHOOT}} （2-2-21）$

$C_{o\_3} \ge \frac {2 \times 10^(-3) \times 5^2}{2 \times 24 \times 1.175} \approx 425.5319uF （2-2-22）$

输出电容损耗计算：
输出电容有效值电流计算：

$I_{Co\_RMS\_MAX} = I_o \ast \frac {r_{Ui\_MAX}}{\sqrt {12}} = 2.2 \times \frac {0.12}{\sqrt {12}} = 76.2102mA （2-2-23）$

$I_{Co\_RMS\_MIN} = I_o \ast \frac {r_{Ui\_MIN}}{\sqrt {12}} = 2.2 \times \frac {0.096}{\sqrt {12}} = 60.9682mA （2-2-24）$

功耗计算：

$P_{Co\_MAX} = I_{Co\_RMS\_MAX}^2 \ast ESR = 76.2102^2 \times 0.05 = 0.2904mW （2-2-25）$

$P_{Co\_MIN} = I_{Co\_RMS\_MIN}^2 \ast ESR = 60.9682^2 \times 0.05 = 0.1859mW （2-2-26）$

输出电容损耗取最恶劣情况做参考。
综上，理论的输出电容值 $C_o$ 为400uF，值得说明的一点，以上的计算均为理论推算，参数也有选取上的偏差。但是，不妨碍我们选电容，理论为400uF，我们可以选470uF的电容，也可以选用两个220uF并联，甚至是多个并联，这里，我推荐后一种，这样就算是高ESR电容，两个并联也可以有效减小ESR值，同时耐压值比最大电压高出20%~50%。我选择330uF 50V贴片固态电解电容，三个并联。
输入电容参数计算：
输入电容一般要保证输入电压纹波峰峰值保持在输入电压的5%~10%以下，因此输入电容也会影响BUCK电路的工作稳定性。由于我们是使用锂电池，所以这个输入电压纹波值较小。不过还是给出一个值：要求输入电压纹波峰峰值为2%，同时也是防止电压纹波从输出端口传递到输入端口造成干扰。假设输入电压最高时，纹波最大。将式（2-2-27）（2-2-28）求得输入电压纹波峰峰值和最大输入电压下，对应输出电压的占空比 $D_{IDEAL\_Ui\_MAX}$ 代入式（2-2-29）。

$V_{RIPP\_PP\_MAX} = 2% \ast U_{i\_MAX} = 2% \times 25 = 0.5V （2-2-27）$

$D_{IDEAL\_Ui\_MAX} = \frac {U_O}{U_{i\_MAX}} = \frac {18}{25} = 0.72 （2-2-28）$

$\begin{equation}\begin{split} C_i&= \frac {I_o \ast D_{IDEAL\_Ui\_MAX} \ast (1-D_{IDEAL\_Ui\_MAX})}{f \ast (V_{RIPP\_PP\_MAX} - ESR \ast I_o \ast (1 + (0.5 \ast r_{Ui\_MAX})))}\\ &= \frac {2.2 \times 0.72 \times (1-0.72)}{10^4 \times (0.5 - 0.05 \times 2.2 \times (1 + (0.5 \times 0.12)))} \approx 0.0065mW\\ \end{split}\end{equation} (2-2-29)$

输入电容损耗计算：
输入电容有效值电流计算：

$\begin{equation}\begin{split} I_{Ci\_RMS\_MAX}&= I_o \ast \sqrt {D_{IDEAL\_Ui\_MAX} \ast (1-D_{IDEAL\_Ui\_MAX} + \frac {r_{Ui\_MIN}^2}{12})}\\ &= 5 \times \sqrt {0.96 \times (1-0.96 + \frac {0.015^2}{12})} = 0.9800A\\ \end{split}\end{equation} (2-2-30)$

$\begin{equation}\begin{split} I_{Ci\_RMS\_MIN}&= I_o \ast \sqrt {D_{IDEAL\_Ui\_MIN} \ast (1-D_{IDEAL\_Ui\_MIN} + \frac {r_{Ui\_MAX}^2}{12})}\\ &= 2.2 \times \sqrt {0.7660 \times (1-0.7660 + \frac {0.12^2}{12})} = 0.9338A\\ \end{split}\end{equation} (2-2-31)$

其中 $r_{Ui\_MIN}$ 与计算 $C_o$ 时的 $r_{D\_MAX}$ 是一样的， $r_{Ui\_MIN}$ 与 $r_{D\_MIN}$ 同理（上述两式对应两种 $U_o$ ）

$P_{Ci\_MAX} = I_{Ci\_RMS\_MAX}^2 \ast ESR = 0.9800 ^2 \times 0.05 = 48.0200mW （2-2-32）$

$P_{Ci\_MIN} = I_{Ci\_RMS\_MIN}^2 \ast ESR = 0.9338^2 \times 0.05 = 43.5991mW （2-2-33）$

输入电容损耗取最恶劣情况做参考。
因此，我选择82uF 35V贴片固态电解电容，两个并联。容的种类繁多，开关电源电路推荐多层式陶瓷电容（MLCC），固态电容，钽电容，铝电解电容。推荐度按顺序递减，自己查阅相关参数便会明白原因。最后，必须要说明的一点，对于BUCK和BUCK-BOOST电路，输入电容的最大有效值电流出现在D=0.5，对于BOOST电路，这个值是1，但是工程上占空比不超过0.9。因此，上述计算的取值都是偏向D=0.5。以上便是超级电容主要的设计思路和理论分析过程。

参考资料：
[1] 周岩,张俊波,陈麒米.开关变换器功率电感磁损建模及应用[J]. 电力自动化设备,2017,37(11):132-135.
[2] 马文超. BUCK电路外围器件参数选型分析[J]. 电子与封装,2019,19(12):30-31.
[3] Sanjaya Maniktala.Switching Power Supplies A-Z,2E[M]. Beijing: The Posts and Telecommunications Press,2015:47-80.